Chapter 7.1: ML workflow basics

7.1 Basics

  1. [E] Explain supervised, unsupervised, weakly supervised, semi-supervised, and active learning.
    • Supervised learning requires labelled input and output data. We are trying to learn a function that maps an input to an output, such that it can predict the label given the input
    • Unsupervised learning has no labelled data but instead tries to discover structures and patterns in the data
    • Weakly supervised learning is supervision with noisy/imprecise labels which are cheaper than hand-labelling data. Though imperfect, weak lables can still generate a precise model
      • Weak labels can come from i) Alternate dataset or pre-trained models, ii) Crowdsourcing iii) Heuristics rules from subject-matter input.
    • Semi-supervised learning is when you have a dataset that is partially labeled and partially unlabeled.

    • Self-supervised learning: Learn representations from unlabbeled data, which can the be used as a pre-trained model on downstream tasks:

      Self-supervised learning obtains supervisory signals from the data itself, often leveraging the underlying structure in the data. The general technique of self-supervised learning is to predict any unobserved or hidden part (or property) of the input from any observed or unhidden part of the input

      https://ai.facebook.com/blog/self-supervised-learning-the-dark-matter-of-intelligence/

      https://ai.stackexchange.com/questions/12266/what-is-the-relation-between-semi-supervised-and-self-supervised-visual-represen

  2. Empirical risk minimization.

    1. [E] What’s the risk in empirical risk minimization?

      We don’t know how well an algorithm will work in practice (its bound on performance) since we don’t know the true distribution of data it will work on

    2. [E] Why is it empirical?

      Empirical means we try to minimise the risk (error) based on a sample set S of the distribution D, where we believe the sample used is a representative of the true distribution the model will work on

    3. [E] How do we minimize that risk?

      By searching for a function $f^*$ which given an input x, the output is as close as possible to the true output y (low risk)

      By using more samples, we make the emperical risk closer to the true risk

  3. [E] Occam’s razor states that when the simple explanation and complex explanation both work equally well, the simple explanation is usually correct. How do we apply this principle in ML?

    In the related concept of overfitting, excessively complex models are affected by statistical noise (a problem also known as the bias-variance trade-off), whereas simpler models may capture the underlying structure better and may thus have better predictive performance.

    So complex models are more prone to overfit on the training data, while simpler models, with equal training performance as the complex ones, are likely to have better predictive performance on unseen data

  4. [E] What are the conditions that allowed deep learning to gain popularity in the last decade?
    • Rise in compute power (Moore’s law)
    • Training datasets
    • Research & new algorithms (CNN, RNN e.t.c)
    • Open source tools

  5. [M] If we have a wide NN and a deep NN with the same number of parameters, which one is more expressive and why?

    I’d first read “expensive”.

    it is more computationally effective to widen the layers than have thousands of small kernels as GPU is much more efficient in parallel computations on large tensors.

    i.e., Wider networks allow parallel computations

    https://stats.stackexchange.com/questions/214360/what-are-the-effects-of-depth-and-width-in-deep-neural-networks

    Wide shallow networks are good at memorization abut not good at generalization

    Multiple layers are better at generalizing as they can learn all the intermediate features at various levels of abstraction. They would be more expressive as they generalize better.

    Aside from the specter of overfitting, the wider your network, the longer it will take to train.

    So wider networks would be more “expensive”

  6. [H] The Universal Approximation Theorem states that a neural network with 1 hidden layer can approximate any continuous function for inputs within a specific range. Then why can’t a simple neural network reach an arbitrarily small positive error?

    A feedforward network with a single layer is sufficient to represent any function, but the layer may be infeasibly large and may fail to learn and generalize correctly.— Ian Goodfellow, DLB

    A function may need a large number of parameters to approximate, and with a single layer, this will make it too big to learn (so may memorize data) and generalize

  7. [E] What are saddle points and local minima? Which are thought to cause more problems for training large NNs?

    • Saddle points are points where a function has a local maximum in one direction and a local minimum in the other direction — the slopes in orthogonal directions are all zero, but it’s not a global maxima or minima. (the points where the derivative is zero or close to zero) are saddle points)

      https://www.kdnuggets.com/2015/11/theoretical-deep-learning.html (last phrase)

    • Local minimum is the smallest value of a function within a given range (local region) but not the entire domain of the function (global)

    • Local minima causes more problems in the optimizer getting stuck. This may be because:

      local minima are very close to global minima in terms of objective functions, [and large functions have their probability concentrated between the index (the critical points) and the objective function]

      thus the model is likely to get stuck and unable to escape

      The local minimum problem is solved by using momentum — adding a fraction of the past weight update to the current update; if the current gradient is zero, the previous one was probably not

      The randomness of stochastic gradient descent also helps escape local minima

  8. Hyperparameters.

     [E] What are the differences between parameters and hyperparameters?
 [E] Why is hyperparameter tuning important?
 [M] Explain algorithm for tuning hyperparameters.

    Parameters are the weights a model is trying to learn to fit a certain function to an output given a certain input. Hyperparameters are the training configurations, such as the bath size

    Hyperparemeter tuning helps arrive at a set of configurations that would enable the model to learn (meet the optimization metric) while maintaining performance stability. [A good set of hyperparameters will also make the training process make optimal use of the compute resources]

    Algorithm for tuning:

    Grid search, random search, bayesian optimization

    • Algorithms

      1. Grid Search

      • Requires manually specifed values for the hyperparameters being tuned

        e.g

        c = [1, 2, 3] d = [0.3, 0.5, 0.7]

      • The search iterates over the cartesian plane of the hyperparameter sets using each pair c[i], d[j] for training. The configuration with the highest validation-score on a held-out set is selected

      2. Random search

      • Combinations of hyperparameter pairs are done randomly.

        It can outperform Grid search, especially when only a small number of hyperparameters affects the final performance of the machine learning algorithm.

      • Applied to continuous and discrete spaces

      3. Bayesian optimisation

      • Builds a probabilistic model mapping from the hyperparameter combinations to the objective evaluated on validation
      • Configurations are selected based on the belief on the current model, which is then updated
      • Balances between exploration and exploitation of current near-optimal configurations

      4. Evolutionary optimisation

      • Uses evoluationary algorithms to mutate and evaluate an initial-random population of hyperparameters

    https://neptune.ai/blog/hyperparameter-tuning-in-python-a-complete-guide-2020

    https://en.wikipedia.org/wiki/Hyperparameter_optimization

  9. Classification vs. regression.

    1. [E] What makes a classification problem different from a regression problem?

      A classification has the output as a discrete number of classes — the function is tryng to predict the probability of the input belonging to each class

      while

      a regression problem has the model try a extrapolate a set of continous future variables by learning the relationship between an existing set of inputs and outputs of the function being learnt

    2. [E] Can a classification problem be turned into a regression problem and vice versa?

      Yes, a label can be converted to a range and a range can be binned/labelled

      • But it’s a bad idea to turn classification to regression.
      • Logistic regression predicting probabilities (classification) is still regression. There’s just a threshold for the probability e.g $p > 0.5$ that makes it classification. However “true” classification algorithms like svm predict a binary outcome, not a proability

      • So the question is actually “Can we replace classification linear regression?” To which the answer is “It woudn’t work” because linear regression extrapolates the value of x and would have to change the hypothesis every time a new sample arrives — you are fitting an extrapolation line, which shifts for each sample. A decision boundary (as with classification) doesn’t move

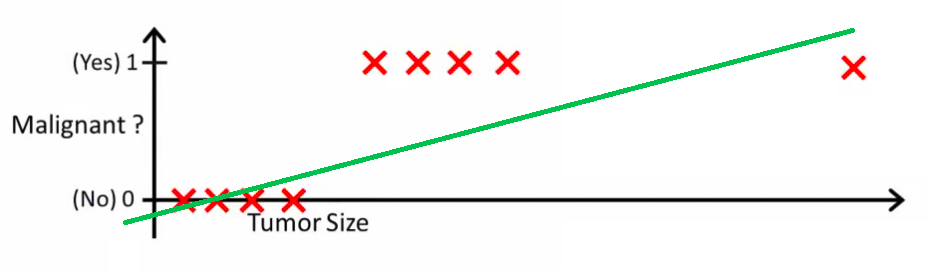
        Linear Regression for Classification

        Figure 1: Linear regression for classification

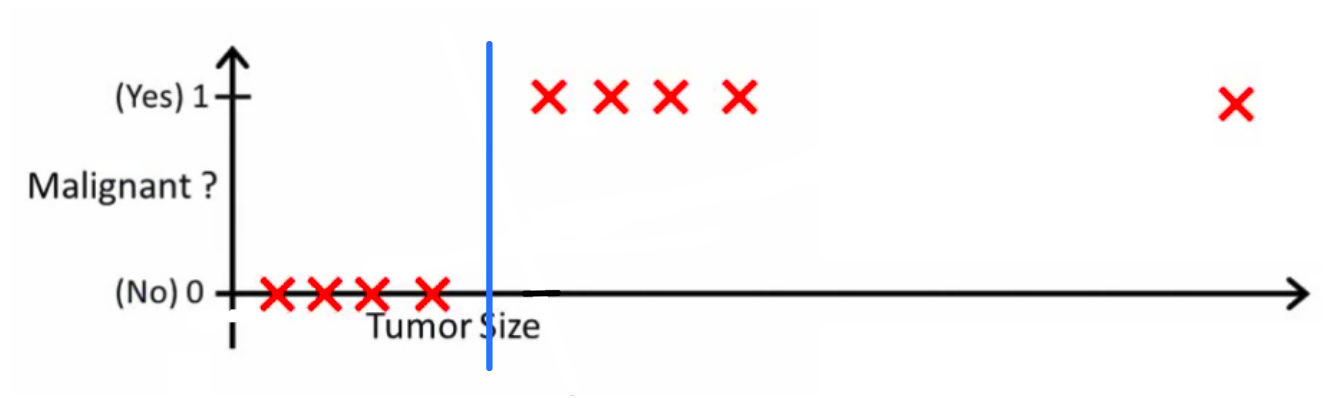
        Logistic Regression

        Figure 2: Logistic regression

        Images from the link below

        See:

        https://stats.stackexchange.com/questions/22381/why-not-approach-classification-through-regression

  10. Parametric vs. non-parametric methods.

    1. [E] What’s the difference between parametric methods and non-parametric methods? Give an example of each method.

      A parametric method uses a fixed number of parameters to determine a probability model while a non-parametric method uses a variable number of parameters

    2. [H] When should we use one and when should we use the other?

      • If there’s an option between a parametric and a non-parametric model both serving the same purpose, e.g Clustering (K-means, K-NN), the most important factor to consider (I think) is the underlying distribution made by the data compared to the assumptions made by each method
        • e.g K-means assumes:
          1. the data is normally distributed, but will still cluster (instead of telling you the data doesn’t cluster) uniform data
          2. Each cluster is spherical/Gaussian

          3. Clusters are evenly sized

            From: https://stats.stackexchange.com/questions/133656/how-to-understand-the-drawbacks-of-k-means/

          e.t.c. So clustering with K-means when the data doesn’t meet these assumptions give wrong good-looking results. In such a case a non-paramatric method would be better suited

      • Other considerations:
        • Parametric need less data while non-parametric methods need lots of data
        • Parametric are slower to train compared to non-parametric

        The use of non-parametric methods may be necessary when data have a ranking but no clear numerical interpretation, such as when assessing preferences. e.g .. movie reviews receiving one to four stars https://en.wikipedia.org/wiki/Nonparametric_statistics

        When the relationship between the response and explanatory variables is known, parametric regression models should be used. If the relationship is unknown and nonlinear, nonparametric regression models should be used https://www.colorado.edu/lab/lisa/services/short-courses/parametric-versus-seminonparametric-regression-models

        So non-parametric is suited when the data has no distribution, or is in ranks, or there are outliers in the data

  11. [M] Why does ensembling independently trained models generally improve performance?

    Ensembles give better predictions compared to using a single model.

    This is because they reduce the variance of the prediction error — they shift the distribution of the prediction space, rather than shrink its spread

    • It works in the context of bias-variance tradeoff— the variance of the prediction error is reduced by adding some bias

    https://machinelearningmastery.com/why-use-ensemble-learning/

  12. [M] Why does L1 regularization tend to lead to sparsity while L2 regularization pushes weights closer to 0?
    • L1 requires minimising the sum between absolute values and the target variable. “Absolute” means the concern is only about the largest value between the feature and the target; other training features with smaller values are ignored
    • This gives sparse estimates. It’s used for variable selection, useful for removing irrelevant features in high-dimensional data
    • L2 adds a regulariser weight between the input variable x_i and the output y_i to prevent coefficients from being zero. Important features are assigned higher weights. Smaller and smaller grad steps are taken as grad approaches zero, thus the low-weighted values are close to zero but not zero

    See: https://stats.stackexchange.com/a/159379

  13. [E] Why does an ML model’s performance degrade in production?

    Distribution shift in the input data over time

  14. [M] What problems might we run into when deploying large machine learning models?
    • Long inference time
    • Problems fitting the model in end-user devices
    • Getting enough data to make updates
    • Building an infrastructure to alert when something goes wrong
  15. Your model performs really well on the test set but poorly in production.

    1. [M] What are your hypotheses about the causes?

      Concept drift in production or distribution mismatch between the test data and the production data

    2. [H] How do you validate whether your hypotheses are correct?

      Train the model and data generated X weeks/months ago and compare its performance between old and new data

    3. [M] Imagine your hypotheses about the causes are correct. What would you do to address them?

      • Update the goal of the prediction to match the new concept in production
      • Update the model with newer data or re-train if the drift can’t be bridged with updates